데이터 사이언스/알고리즘
버블 정렬 (Bubble Sort)
데이터분석가 이채은
2025. 2. 10. 19:36
버블 정렬
"옆에 있는 요소와 비교하며 swap(교환)하여 정렬하는 가장 기초적인 정렬 알고리즘"
- 큰 값이 거품(Bubble)처럼 밀려 올라가는 방식
- 가장 단순한 정렬 방법이지만, 성능이 좋지 않아 실무에서는 거의 사용되지 않음
버블 정렬 동작 원리
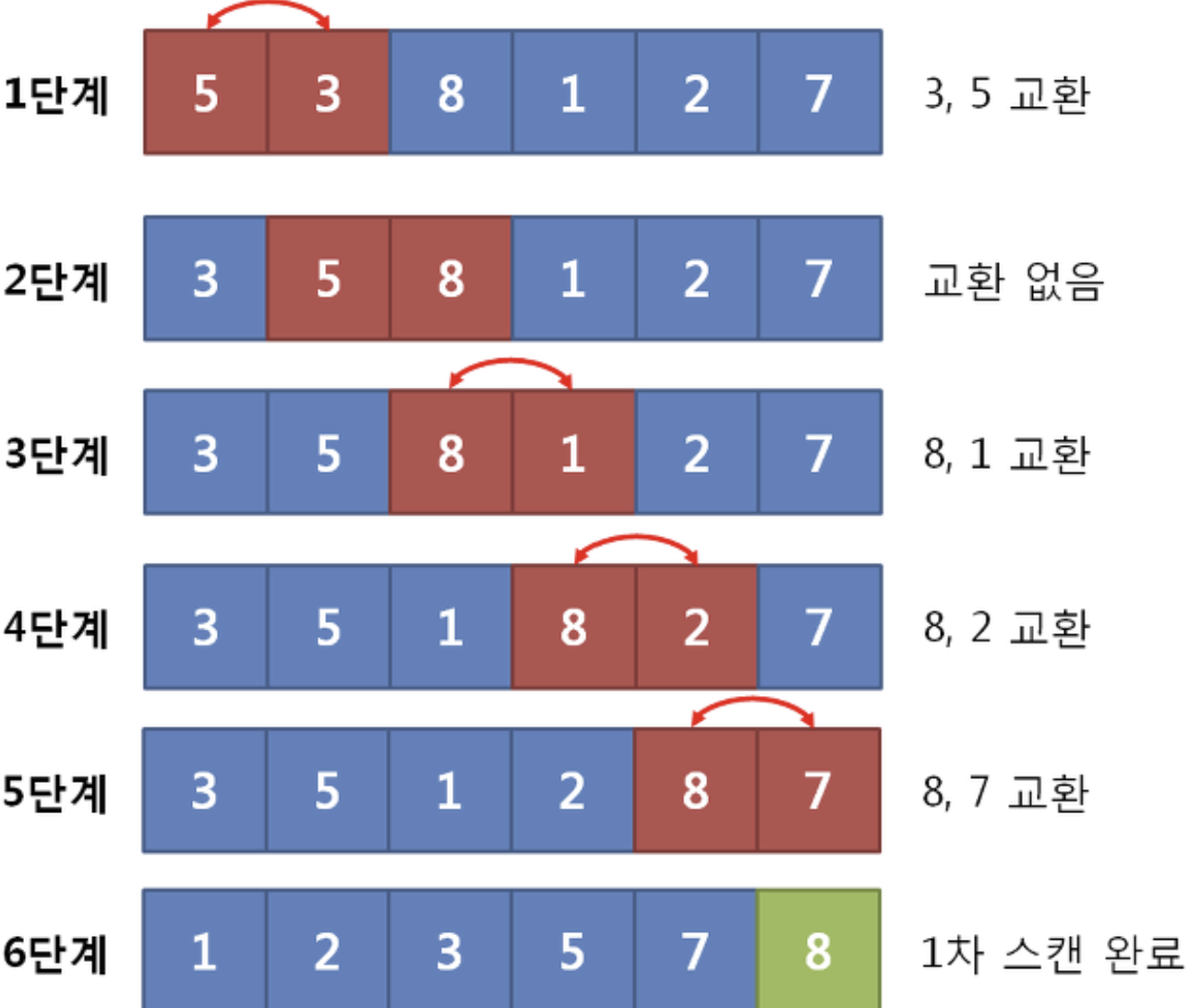
- 리스트의 처음부터 시작하여 인접한 두 개의 값을 비교
- 만약 앞의 값이 크다면, 두 값을 교환 (swap)
- 리스트의 끝까지 반복하면 가장 큰 값이 맨 뒤로 이동
- 위 과정을 반복하여 정렬이 완료될 때까지 진행
# Pseudo Code
FUNCTION BubbleSort(arr)
FOR i FROM 0 TO length(arr) - 1
swapped = FALSE
FOR j FROM 0 TO length(arr) - i - 1
IF arr[j] > arr[j + 1] THEN
SWAP arr[j] AND arr[j + 1]
swapped = TRUE
END FOR
IF swapped = FALSE THEN
BREAK
END FOR
RETURN arr
END FUNCTION
# Full Code
def bubble_sort(arr):
n = len(arr)
for i in range(n - 1): # 총 n-1번 반복
swapped = False # 교환이 일어났는지 확인하는 변수
for j in range(n - 1 - i): # 정렬된 부분을 제외하고 비교
if arr[j] > arr[j + 1]: # 앞쪽 값이 크면 교환
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
if not swapped: # 만약 교환이 없었다면 이미 정렬됨
break
return arr
# 테스트
arr = [5, 3, 8, 4, 2]
print("버블 정렬 결과:", bubble_sort(arr))버블 정렬의 시간복잡도
| 경우 | 시간 복잡도 |
| 최선 (이미 정렬됨) | O(n) |
| 평균 | O(n²) |
| 최악 (역순 정렬) | O(n²) |
✅ 최선의 경우 O(n)
- 리스트가 이미 정렬된 경우, 한 번만 검사하면 끝
❌ 평균 & 최악의 경우 O(n²)
- 이중 반복문이 사용되므로 n(n-1)/2번 비교 → O(n²)
- 입력 크기가 커질수록 성능이 급격히 떨어짐
버블 정렬의 장단점
장점
- 구현이 쉽고 직관적
- 이미 정렬된 경우 빠르게 종료 가능(O(n))
- 추가 메모리 사용이 적음(O(1), 제자리 정렬)
단점
- O(n²)로 매우 비효율적 (실무에서 거의 사용되지 않음)
- 다른 정렬(퀵 정렬, 병합 정렬) 보다 훨씬 느림
📌 결론
버블 정렬은 이해하기 쉽지만, 매우 비효율적이므로 실무에서는 잘 사용되지 않는다. 대신 퀵 정렬(O(n log n)) 또는 병합 정렬(O(n log n)) 같은 더 효율적인 알고리즘을 사용한다.
버블 정렬은 기본적인 정렬 알고리즘 개념(비교, 교환, 반복)의 이해를 돕고, 다른 정렬 알고리즘(퀵 정렬, 병합 정렬 등)과의 성능 비교를 위해 학습됩니다.