The Geometric Distribution (기하 분포)

기하 분포

기하 분포(Geometric Distribution)는 처음으로 성공할 때까지 시행한 횟수를 모델링하는 확률 분포이다.

연속된 베르누이 시행에서 처음 성공(1)이 나올 때까지 몇 번의 실패(0)를 거치는지를 나타내는 분포로 성공할 때까지 걸리는 시행 횟수를 분석할 때 사용한다.

출처: https://www.mathworks.com/help/stats/geometric-distribution.html

---

기하 분포의 확률 질량 함수 (PMF)

확률 변수가 X가 기하 분포를 따른다면:

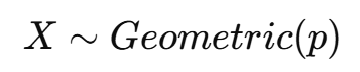
기하 분포의 확률 질량 함수(PMF)는:

여기서:

• p = 단일 시행에서 성공할 확률
• k = 성공이 처음 나타나는 시행의 횟수

첫 성공이 k번째 시행에서 나올 확률은, k−1번의 실패 후 성공하는 경우이다.

---

기하 분포의 누적 분포 함수 (CDF)

누적 분포 함수(CDF)는 특정 값 이하에서 성공이 발생할 확률을 나타낸다.

이를 계산하면:

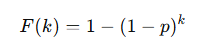
기하 분포의 CDF 공식:

 

설명:

 

• 성공이 1번째 시행에서 발생할 확률: p
• 성공이 1~2번째 시행에서 발생할 확률: p + (1 − p)p
• 성공이 1~k번째 시행에서 발생할 확률: 1 − (1 − p)^k
  (즉, k번 모두 실패할 확률을 빼는 방식!)

 

---

기댓값과 분산

기하 분포의 기댓값(평균)과 분산은 다음과 같은 공식으로 구할 수 있다:

---

기하 분포의 활용

• 고객 서비스: 고객이 전화를 걸었을 때, 첫 번째 상담원이 응답할 때까지 걸리는 시간
• 스포츠 분석: 농구 선수가 첫 번째 슛을 성공하기까지의 시도 횟수
• 도박 및 베팅: 첫 번째 당첨이 나올 때까지의 시도 횟수

기하 분포는 첫 성공까지 걸리는 시행 횟수를 예측하는 데 유용하므로 베르누이 시행이 독립적일 때 적용 가능하다.

---

예제 1: 주사위를 던져 처음 6이 나오는 시행 횟수

주사위를 던질 때, 처음으로 6이 나올 때까지 던진 횟수 X가 기하 분포를 따른다고 하자.

• 성공 (6이 나올 확률) : p = 1/6​
• 실패 (1, 2, 3, 4, 5 나올 확률) : 1 − p = 5/6
  
  첫 6이 3번째 시행에서 나올 확률을 구해보자. ​

 

즉, 처음으로 6이 3번째 던지기에서 나올 확률은 약 11.6%이다.

---

예제: 동전을 던져 앞면이 처음 나오는 시행 횟수의 CDF

예제: 앞면이 나올 확률이 p = 0.5인 동전을 던진다고 하자.
최초로 앞면이 나오는 시행 횟수가 k ≤ 3일 확률을 구하자.

 

공식 적용

즉, 동전을 던질 때 처음으로 앞면이 3번째 시행 이내에 나올 확률은 87.5%이다.