데이터 사이언스/수리 통계학
Joint and Marginal Distributions (결합 및 주변 분포)
데이터분석가 이채은
2025. 3. 28. 14:25
결합 분포(Joint Distribution)와 주변 분포(Marginal Distribution)는 두 개 이상의 확률 변수가 함께 어떻게 분포하는지를 이해할 때 핵심이 되는 개념이다.
결합 분포란? (Joint Distribution)
결합 분포는 두 확률 변수 X와 Y가 동시에 어떤 값을 가질 확률을 나타내는 함수이다.
- 이산형 확률 변수의 경우:
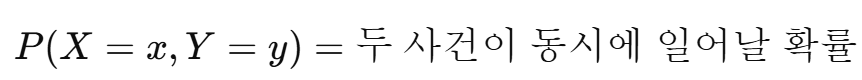
이를 결합 확률 질량 함수 (Joint PMF)라고 한다.
- 연속형 확률 변수의 경우:
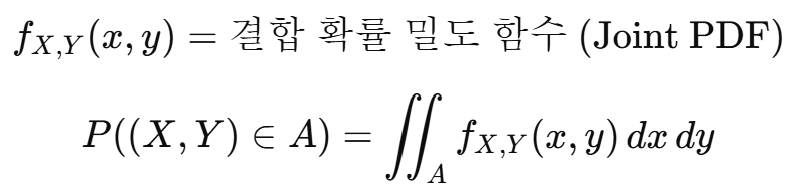
즉, 두 변수의 관계를 함께 고려하는 분포이다.
주변 분포란? (Marginal Distribution)
주변 분포는 다변량 확률 분포에서 특정 변수 하나만 따로 떼어내어 보는 분포이다.
다른 변수의 값을 고려하지 않고, 전체 분포에서 그 변수를 "통합(integrate out)"해서 얻는다.
이산형일 경우

연속형일 경우
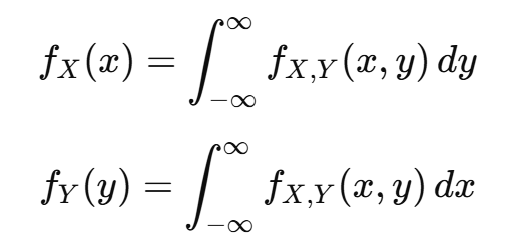
결합 분포에서 다른 변수의 축을 적분/합산하여 제거하면 주변 분포가 된다.
예제 1: 이산형 결합 분포
| X \ Y | 1 | 2 | 3 |
| 1 | 0.1 | 0.2 | 0.3 |
| 2 | 0.3 | 0.4 | 0.7 |
| 합 | 0.4 | 0.6 | 1.0 |

예제 2: 연속형 결합 분포
fX,Y(x, y) = 6xy on 0 ≤ x ≤ 1, 0 ≤ y ≤ 1
이때, fX(x)를 구해보자.
