Tags
- 쟝고
- 큐
- delete
- drf
- SQL
- count
- 뷰
- update
- M:N
- Django
- 통계학
- regexp
- outer join
- 이진트리
- migrations
- Article & User
- N:1
- stack
- DB
- Tree
- Vue
- 백트래킹
- distinct
- Queue
- 완전검색
- ORM
- 스택
- 트리
- 그리디
- create
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
The Geometric Distribution (기하 분포) 본문
기하 분포
기하 분포(Geometric Distribution)는 처음으로 성공할 때까지 시행한 횟수를 모델링하는 확률 분포이다.
연속된 베르누이 시행에서 처음 성공(1)이 나올 때까지 몇 번의 실패(0)를 거치는지를 나타내는 분포로 성공할 때까지 걸리는 시행 횟수를 분석할 때 사용한다.
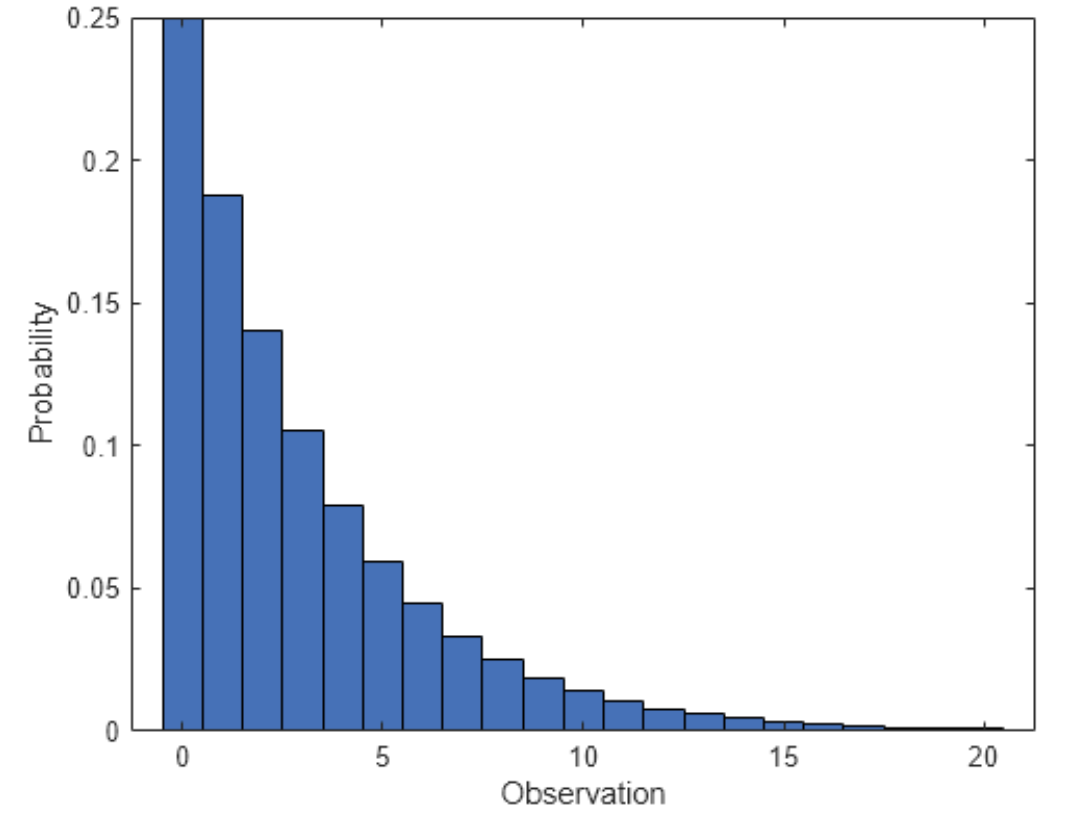
기하 분포의 확률 질량 함수 (PMF)
확률 변수가 X가 기하 분포를 따른다면:

기하 분포의 확률 질량 함수(PMF)는:
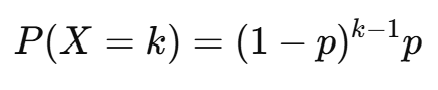
여기서:
- p = 단일 시행에서 성공할 확률
- k = 성공이 처음 나타나는 시행의 횟수
첫 성공이 k번째 시행에서 나올 확률은, k−1번의 실패 후 성공하는 경우이다.
기하 분포의 누적 분포 함수 (CDF)
누적 분포 함수(CDF)는 특정 값 이하에서 성공이 발생할 확률을 나타낸다.
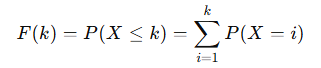
이를 계산하면:
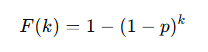
기하 분포의 CDF 공식:

설명:
- 성공이 1번째 시행에서 발생할 확률: p
- 성공이 1~2번째 시행에서 발생할 확률: p + (1 − p)p
- 성공이 1~k번째 시행에서 발생할 확률: 1 − (1 − p)k
(즉, k번 모두 실패할 확률을 빼는 방식!)
기댓값과 분산
기하 분포의 기댓값(평균)과 분산은 다음과 같은 공식으로 구할 수 있다:

기하 분포의 활용
- 고객 서비스: 고객이 전화를 걸었을 때, 첫 번째 상담원이 응답할 때까지 걸리는 시간
- 스포츠 분석: 농구 선수가 첫 번째 슛을 성공하기까지의 시도 횟수
- 도박 및 베팅: 첫 번째 당첨이 나올 때까지의 시도 횟수
기하 분포는 첫 성공까지 걸리는 시행 횟수를 예측하는 데 유용하므로 베르누이 시행이 독립적일 때 적용 가능하다.
예제 1: 주사위를 던져 처음 6이 나오는 시행 횟수
주사위를 던질 때, 처음으로 6이 나올 때까지 던진 횟수 X가 기하 분포를 따른다고 하자.
- 성공 (6이 나올 확률) : p = 1/6
- 실패 (1, 2, 3, 4, 5 나올 확률) : 1 − p = 5/6

즉, 처음으로 6이 3번째 던지기에서 나올 확률은 약 11.6%이다.
예제: 동전을 던져 앞면이 처음 나오는 시행 횟수의 CDF
예제: 앞면이 나올 확률이 p = 0.5인 동전을 던진다고 하자.
최초로 앞면이 나오는 시행 횟수가 k ≤ 3일 확률을 구하자.
공식 적용

즉, 동전을 던질 때 처음으로 앞면이 3번째 시행 이내에 나올 확률은 87.5%이다.
'데이터 사이언스 > 수리 통계학' 카테고리의 다른 글
| Continuous Random Variables and Continuous Distributions (연속 확률 변수와 연속 확률 분포) (0) | 2025.03.21 |
|---|---|
| The Poisson Distribution (포아송 분포) (2) | 2025.03.20 |
| The Binomial Distribution (이항 분포) (0) | 2025.03.18 |
| The Categorical Distribution (범주형 분포) (0) | 2025.03.17 |
| The Bernoulli Distribution (베르누이 분포) (0) | 2025.03.16 |



