Tags
- SQL
- 백트래킹
- 이진트리
- create
- 트리
- Django
- delete
- regexp
- stack
- Article & User
- 큐
- 스택
- update
- Vue
- count
- migrations
- Queue
- 완전검색
- ORM
- 그리디
- outer join
- 통계학
- N:1
- M:N
- drf
- DB
- distinct
- 쟝고
- Tree
- 뷰
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
The Poisson Distribution (포아송 분포) 본문
포아송 분포
포아송 분포(Poisson Distribution)는 특정 시간 또는 공간 내에서 사건이 발생하는 횟수를 모델링하는 확률 분포이다.
일정한 시간 동안 특정 사건이 몇 번 발생하는지를 예측하는 데 사용되므로 주어진 시간 또는 공간에서 발생하는 사건의 수를 세는 데 적합하다.

예시:
- 은행 창구에서 1시간 동안 방문하는 고객 수
- 웹사이트에서 1분 동안 발생하는 방문자 수
- 병원 응급실에 24시간 동안 도착하는 환자 수
- 축구 경기에서 90분 동안 발생하는 골 수
포아송 분포의 확률 질량 함수 (PMF)
확률 변수가 X가 포아송 분포를 따른다면:

포아송 분포의 확률 질량 함수(PMF)는:
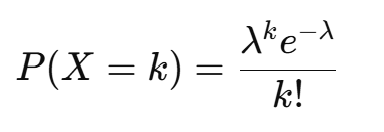
여기서:
- = 사건이 발생하는 횟수 (0, 1, 2, 3,...)
- λ = 단위 시간(공간) 당 평균 발생 횟수
- e = 자연상수 (≈ 2.718)
포아송 분포는 k개의 사건이 발생할 확률을 구하는 데 사용된다.
기댓값과 분산
포아송 분포의 기댓값(평균)과 분산은 매우 간단하다:
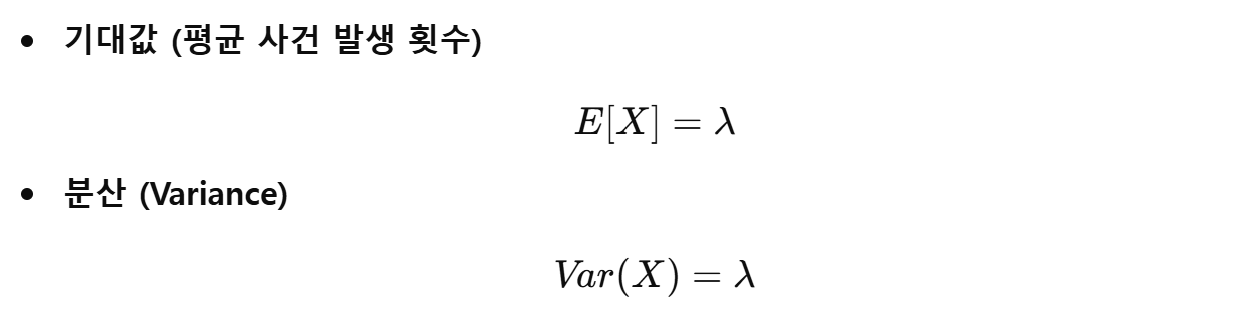
즉, 포아송 분포에서는 평균과 분산이 동일하다.
포아송 분포의 활용
- 콜센터: 1시간 동안 걸려오는 전화 수 예측
- 교통량 분석: 1시간 동안 도로를 지나가는 차량 수 예측
- 유전자 분석: 특정 DNA 변이가 발생하는 횟수 모델링
- 네트워크 보안: 1시간 동안 발생하는 해킹 시도 횟수 예측
포아송 분포는 "희귀한 사건"이 발생하는 패턴을 분석하는 데 매우 유용하다.
예제 1: 고객 방문 수 예측
한 카페에서 1시간 동안 평균 5명의 고객이 방문한다고 하자.
이때, 1시간 동안 정확히 3명의 고객이 방문할 확률을 구해보자.
여기서:
- λ = 5 (평균적으로 1시간에 5명 방문)
- k = 3 (정확히 3명 방문할 확률을 구하려 함)
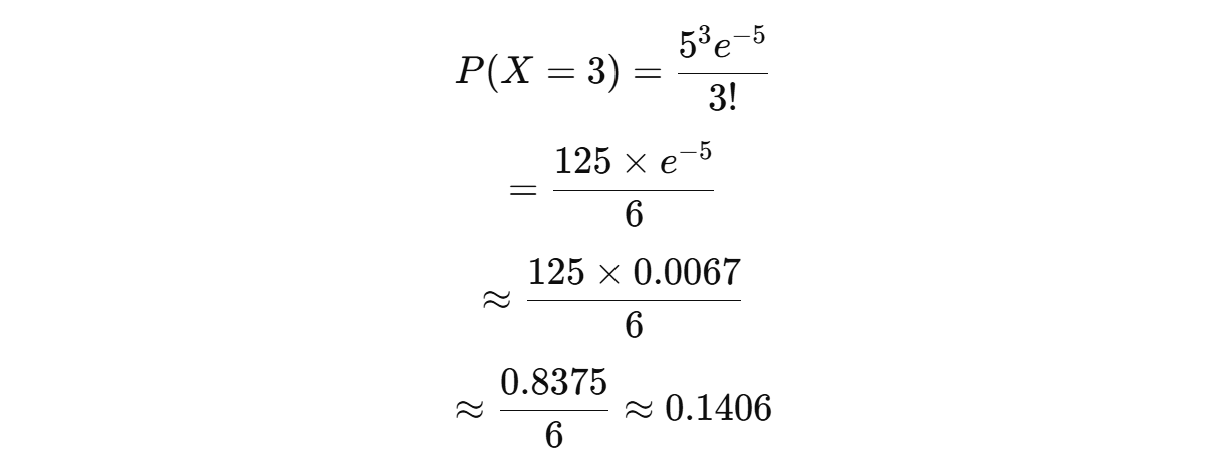
즉, 1시간 동안 정확히 3명의 고객이 방문할 확률은 약 14.1%이다.
'데이터 사이언스 > 수리 통계학' 카테고리의 다른 글
| Probability Density Function and Cumulative Distribution Function (확률 밀도 함수와 누적 분포 함수) (0) | 2025.03.22 |
|---|---|
| Continuous Random Variables and Continuous Distributions (연속 확률 변수와 연속 확률 분포) (0) | 2025.03.21 |
| The Geometric Distribution (기하 분포) (0) | 2025.03.19 |
| The Binomial Distribution (이항 분포) (0) | 2025.03.18 |
| The Categorical Distribution (범주형 분포) (0) | 2025.03.17 |



