- Vue
- outer join
- SQL
- count
- 백트래킹
- 큐
- Tree
- migrations
- 완전검색
- 쟝고
- 뷰
- 트리
- DB
- create
- Queue
- drf
- distinct
- delete
- N:1
- stack
- M:N
- 스택
- ORM
- 이진트리
- Django
- Article & User
- 그리디
- update
- 통계학
- regexp
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
데이터 분석 기술 블로그
Probability Density Function and Cumulative Distribution Function (확률 밀도 함수와 누적 분포 함수) 본문
Probability Density Function and Cumulative Distribution Function (확률 밀도 함수와 누적 분포 함수)
데이터분석가 이채은 2025. 3. 22. 14:25확률 밀도 함수와 누적 분포 함수
연속 확률 변수(Continuous Random Variable)를 다룰 때는 특정 값이 아니라 구간(interval)에 대한 확률을 고려해야 한다. 이를 위해 확률 밀도 함수(PDF)와 누적 분포 함수(CDF) 개념이 필요하다.

확률 밀도 함수 (Probability Density Function, PDF)
확률 밀도 함수(PDF)는 연속 확률 변수의 분포를 나타내는 함수로, 특정 구간에서 확률을 구할 때 사용된다.
즉, 확률이 특정 구간에 얼마나 집중되어 있는지를 나타낸다.
PDF의 특징
- 특정 값에서의 확률 P(X = x)는 항상 0 → P(a ≤ X ≤ b) 형태로 계산해야 함.
- 확률을 구하려면 PDF를 적분해야 함.
- PDF의 총면적(전체 확률)은 1이 되어야 함.
확률 계산 공식

여기서 f(x)는 확률 밀도 함수(PDF)이다.
- PDF는 마치 "높낮이가 있는 언덕"으로 언덕의 특정 지점(특정 값 X)의 높이 자체는 의미가 없음.
- 하지만, 특정 구간(구간 확률)에서의 면적이 확률로 해석됨.
누적 분포 함수 (Cumulative Distribution Function, CDF)
누적 분포 함수(CDF)는 확률 변수가 특정 값 이하일 확률을 나타내는 함수이다.
CDF 정의
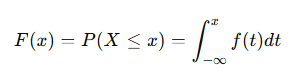
CDF의 특징
- 특정 값 이하의 확률을 누적하여 계산함.
- CDF의 범위는 항상 0 ≤ F(x) ≤ 10
- CDF는 항상 비감소(non-decreasing) 함수
- CDF를 미분하면 PDF가 됨:

- CDF는 "언덕을 오르는 총 높이"로 PDF는 특정 지점의 기울기(언덕의 높낮이)
- CDF는 전체 언덕을 올라갈 때의 누적된 고도
CDF의 성질
1. 확률 범위
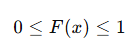
모든 확률은 0과 1사이에 있음
2. 단조 증가 (Monotonic Increasing):

가 커질수록 누적 확률도 증가함.
3. 극한값:

즉, X가 매우 작은 값에서는 확률이 0이고, 매우 큰 값에서는 확률이 1에 가까워짐.
4. PDF와의 관계:
연속 확률 변수의 경우, CDF를 미분하면 PDF가 됨:
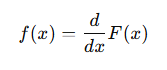
즉, PDF는 CDF의 도함수이다.
또한, 특정 구간에서의 확률은 CDF를 이용해 다음과 같이 구할 수 있다:
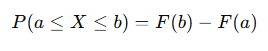
연속 확률 변수의 CDF 정의
연속 확률 변수 X의 CDF는 다음과 같이 정의된다:

여기서:
- f(x) = 확률 밀도 함수 (PDF, Probability Density Function)
- F(x) = 누적 분포 함수 (CDF, Cumulative Distribution Function)
즉, CDF는 특정 값 x까지의 확률을 계산하기 위해 PDF를 적분한 값이다.
특징:
- 는 항상 0과 1 사이의 값을 가짐: 0≤F(x)≤10 \leq F(x) \leq 1
- F(x)F(x)는 단조 증가 함수 (non-decreasing function)
- F(x)F(x)를 미분하면 PDF를 얻을 수 있음:

PDF와 CDF의 관계

- PDF는 확률의 "밀도"
- CDF는 확률의 "누적 값"
연속 확률 분포의 활용
- 자연 현상 분석: 온도, 속도, 길이 등 연속적인 데이터를 모델링
- 신뢰성 분석: 제품의 수명(time-to-failure) 모델링 (예: 기계 부품이 고장 날 확률)
- 금융 데이터 분석: 주식 수익률 분포 모델링
- 통계적 추론: 중심극한정리(CLT)를 활용한 가설 검정
연속 확률 분포를 다룰 때는 특정 값이 아니라 "구간"을 고려해야 한다. PDF를 사용해 분포 형태를 확인하고, CDF를 이용해 누적 확률을 계산하면 된다.
예제: 정규 분포에서 PDF와 CDF 비교
정규 분포 N(0,1) (평균 0, 분산 1)에서:
- PDF는 정규 곡선(벨 모양)
- CDF는 S자 곡선 형태
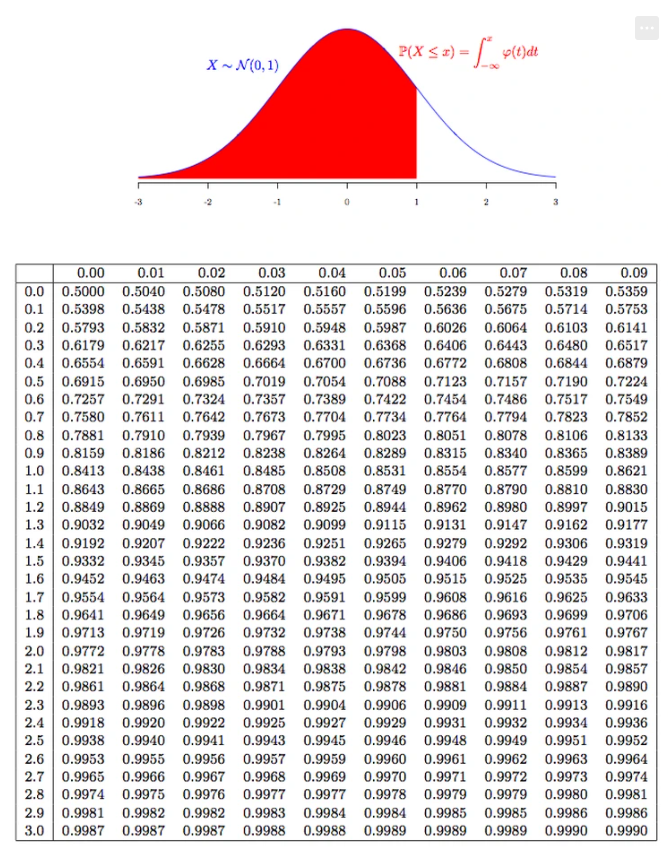
질문 1: P(X ≤ 0)의 값은?
➡ CDF에서 F(0) 값을 확인하면 됨. 정규 분포에서는 약 0.5.
질문 2: P(−1 ≤ X ≤ 1)의 값은?
➡ F(1) − F(−1) 값을 계산하면 됨. 정규 분포에서는 약 0.68 (68%).
결론:
- 특정 값에서의 확률을 계산하려면 PDF를 적분해야 함.
- 하지만 특정 값 이하의 확률을 빠르게 구하려면 CDF를 사용하면 됨.
'데이터 사이언스 > 수리 통계학' 카테고리의 다른 글
| The Exponential Distribution (지수 분포) (0) | 2025.03.24 |
|---|---|
| The Uniform Distribution (균등 분포) (0) | 2025.03.23 |
| Continuous Random Variables and Continuous Distributions (연속 확률 변수와 연속 확률 분포) (0) | 2025.03.21 |
| The Poisson Distribution (포아송 분포) (2) | 2025.03.20 |
| The Geometric Distribution (기하 분포) (0) | 2025.03.19 |



