The Exponential Distribution (지수 분포)

지수 분포

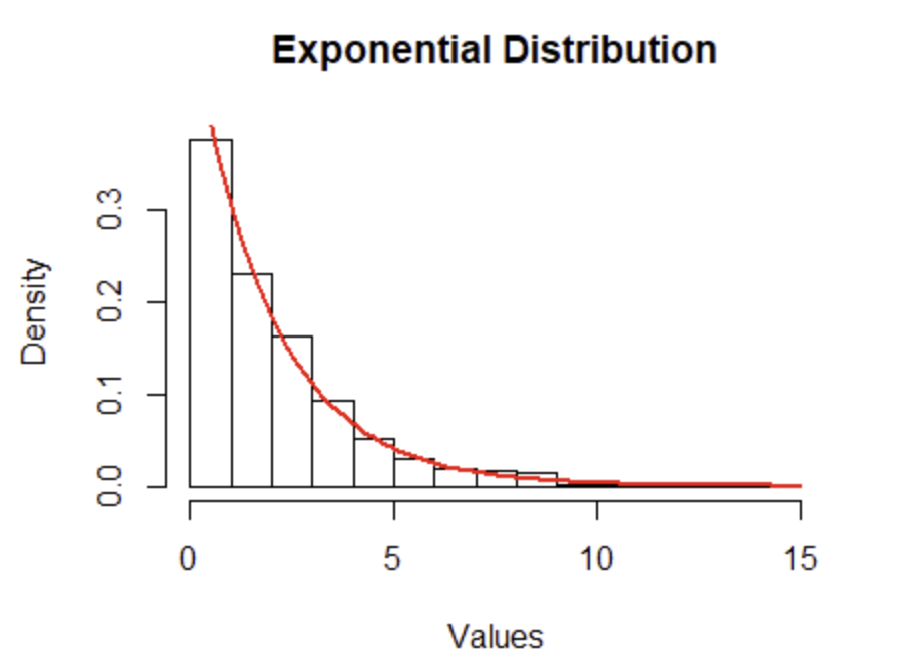
지수 분포(Exponential Distribution)는 어떤 사건이 발생할 때까지 걸리는 시간을 모델링하는 확률 분포이다.
즉, "다음 사건이 언제 발생할 것인가?"를 예측할 때 사용된다.

 

• 사건이 연속적으로 독립적으로 발생할 때, 다음 사건이 발생하기까지의 시간을 모델링하는 분포.
• 평균 발생률(λ\lambdaλ)을 기반으로 사건이 언제 일어날지를 예측.

출처: https://makemeanalyst.com/statistics-with-r/exponential-distribution-in-r-programming/

 

지수 분포가 적용되는 예시

• 버스가 도착할 때까지의 대기 시간
• 콜센터에서 다음 전화가 걸려오기까지의 시간
• 방사성 물질이 붕괴되기까지 걸리는 시간
• 기계가 고장 나기까지의 시간 (수명 분석)

---

확률 밀도 함수 (PDF)

 

여기서:

• λ = 사건이 단위 시간당 발생하는 평균 횟수 (rate parameter)
• x = 사건이 발생할 때까지의 시간

지수 분포는 시간이 지날수록 사건이 발생할 확률이 점점 낮아지는 특징이 있다.

---

누적 분포 함수 (CDF)

즉, 시간이 지나면 누적 확률이 점점 1에 가까워진다.
(어느 순간에는 반드시 사건이 발생할 것이기 때문이다.)

---

기댓값과 분산

---

지수 분포의 특징

기억 없음 성질 (Memoryless Property)

 

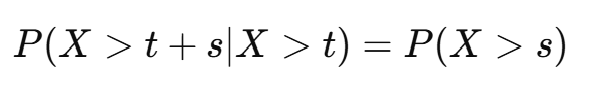
• 즉, 과거의 정보가 현재의 확률에 영향을 미치지 않음!
• 예: 버스를 10분 동안 기다렸다고 해서, 다음 버스가 곧 올 확률이 높아지는 게 아님.

---

포아송 분포와 관계있음

X∼Exponential(λ)이면, 시간 t 동안 k번 사건이 발생할 확률은 포아송 분포 Poisson(λt)를 따름.

---

지수 분포의 활용

• 대기 시간 분석: 버스, 택시, 고객 서비스 센터에서 다음 고객이 올 때까지의 시간 모델링
• 제품 수명 예측: 기계나 부품이 언제 고장 날지를 예측 (신뢰성 분석)
• 생물학적 과정: 방사성 물질의 붕괴 시간 예측

지수 분포는 "다음 사건이 언제 발생할지"를 예측하는 데 매우 유용하다.

---

예제: 버스 도착 시간

예제: 버스가 평균적으로 10분에 한 번씩 도착한다고 하자.
즉, 단위 시간당 도착하는 횟수는 λ = 1/10 = 0.1
5분 이내에 버스가 도착할 확률은?

 

공식 적용

 

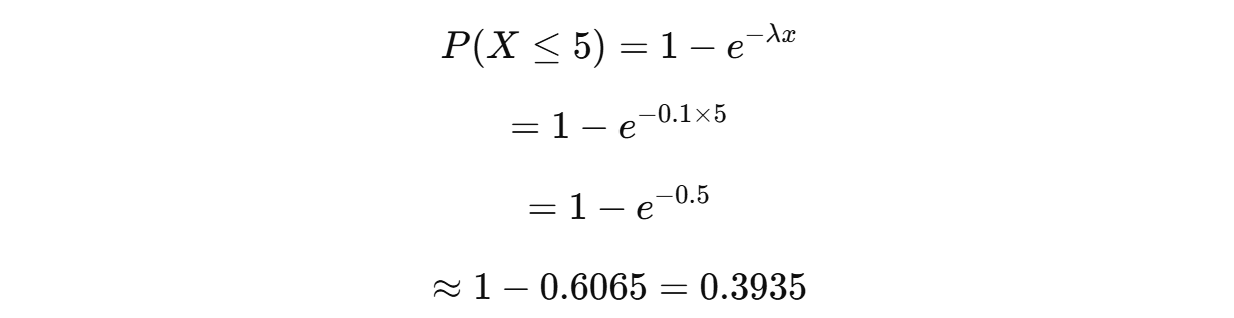
즉, 5분 이내에 버스가 도착할 확률은 약 39.35%이다.