Tags
- Tree
- Vue
- 트리
- stack
- update
- Django
- regexp
- outer join
- Article & User
- 뷰
- 쟝고
- count
- 완전검색
- SQL
- Queue
- 그리디
- M:N
- delete
- N:1
- 통계학
- DB
- migrations
- 백트래킹
- distinct
- 큐
- 스택
- 이진트리
- create
- ORM
- drf
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
The Laplace Distribution (라플라스 분포, 이중 지수 분포) 본문
이중 지수 분포
라플라스 분포(Laplace Distribution) 또는 이중 지수 분포(Double Exponential Distribution)는 평균을 중심으로 대칭적인 확률 분포로, 데이터가 정규 분포보다 중심에 더 집중되고 꼬리가 더 두꺼운(heavy-tailed) 특징이 있다.
- 정규 분포(Gaussian Distribution)와 유사하지만, 중심에서 더 뾰족하고 꼬리가 두꺼운 분포.
- 특정한 점(평균)에서 값이 급격히 변화하는 경우 모델링할 때 적합.
- "변화가 급격하게 발생하는 데이터"를 다룰 때 사용됨.
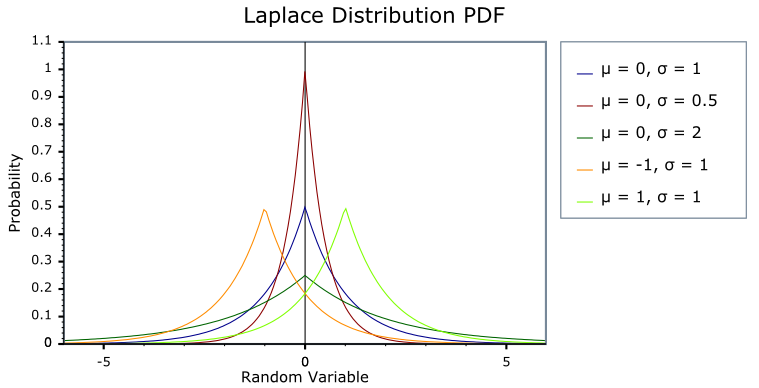
라플라스 분포가 적용되는 예시
- 금융 데이터(주가, 환율 변동) → 정규 분포보다 급격한 변화가 많음.
- 자연어 처리(NLP)에서 오차 모델링 → 단어 빈도수나 감정 분석에서 활용됨.
- 신호 처리 및 이미지 압축 → 변화가 많은 데이터에 적합.
- 가설 검정 및 Bayesian 분석 → 라플라스 사전 분포(Prior)로 사용됨.
확률 밀도 함수 (PDF)

여기서:
- μ = 위치 모수(location parameter, 평균 역할)
- b = 척도 모수(scale parameter, 분산 역할)
- e = 자연상수 (≈ 2.718)
라플라스 분포는 평균(μ)을 중심으로 대칭이며, 기울기가 급격히 변함.
b가 클수록 분포가 더 퍼지고, 작을수록 데이터가 중심에 집중됨.
비교:
- 정규 분포: 중심에서 완만하게 변화, 꼬리가 얇음.
- 라플라스 분포: 중심에서 급격하게 변화, 꼬리가 두꺼움.
누적 분포 함수 (CDF)
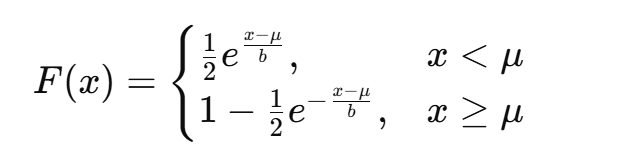
CDF는 정규 분포보다 중심에서 빠르게 증가한다. 따라서 이상값(Outlier)이 있을 때도 상대적으로 강건(Robust)하다.
기댓값과 분산

라플라스 분포의 특징
- 꼬리가 두꺼운 분포 (Heavy-Tailed Distribution)
- 정규 분포보다 극단적인 값(이상값)이 더 자주 발생.
- 금융 데이터, 소셜 미디어 감정 분석 등에서 활용.
- 변화가 급격한 데이터에 적합
- 정규 분포는 점진적인 변화 모델링에 적합하지만,
- 라플라스 분포는 급격한 변화가 포함된 데이터를 잘 설명함.
- 정규 분포보다 이상값(Outlier)에 덜 민감
- 평균보다 중앙값(Median)이 더 중요한 경우에 유용.
- 로버스트(robust) 회귀 분석에서 활용.
라플라스 분포의 활용
- 금융 데이터 분석 → 주가, 환율의 급격한 변동 모델링
- 자연어 처리(NLP) → 감정 분석(Sentiment Analysis) 모델링
- 이미지 압축 및 신호 처리 → 변화가 많은 데이터의 분포 모델링
- 베이지안 분석(Bayesian Analysis) → 강건한 사전 확률(Prior) 분포로 사용
라플라스 분포는 "급격한 변화"를 모델링할 때 강력한 도구이다. 정규 분포와 달리, 중심에서 데이터가 더 집중되고 꼬리가 두꺼운 특성을 가진다.
예제: 금융 데이터 분석
예제: 주가 변동이 평균 100을 중심으로 변화하며, 급격한 변동을 가질 때 모델링
b=10b = 10인 경우, 특정 구간의 확률을 계산해 보자.
구간 확률 계산

정규 분포보다 중심 값에 더 많은 확률이 집중된다.
즉, 급격한 변화를 예측할 때 유용하다.
'데이터 사이언스 > 수리 통계학' 카테고리의 다른 글
| Joint and Marginal Distributions (결합 및 주변 분포) (0) | 2025.03.28 |
|---|---|
| Change of Variables (확률 변수 변환) (0) | 2025.03.27 |
| The Normal Distribution (정규 분포, Gaussian Distribution) (2) | 2025.03.25 |
| The Exponential Distribution (지수 분포) (0) | 2025.03.24 |
| The Uniform Distribution (균등 분포) (0) | 2025.03.23 |




