- 그리디
- Queue
- delete
- Article & User
- N:1
- DB
- 스택
- count
- migrations
- 통계학
- distinct
- Vue
- 완전검색
- 백트래킹
- ORM
- update
- 뷰
- 트리
- Tree
- create
- 이진트리
- outer join
- 큐
- SQL
- 쟝고
- M:N
- drf
- regexp
- stack
- Django
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
데이터 분석 기술 블로그
The Normal Distribution (정규 분포, Gaussian Distribution) 본문
The Normal Distribution (정규 분포, Gaussian Distribution)
데이터분석가 이채은 2025. 3. 25. 14:25정규 분포
정규 분포(Normal Distribution)는 자연 현상에서 가장 많이 나타나는 확률 분포로, 데이터 분석과 통계에서 핵심적인 역할을 한다. 가우스 분포(Gaussian Distribution)라고도 불린다.
- 데이터가 대칭적이고 종 모양(Bell-shaped Curve)을 따르는 확률 분포.
- 평균 근처에 값이 집중되고, 평균에서 멀어질수록 값이 드물게 나타남.
- 중심극한정리(Central Limit Theorem, CLT)에 의해 여러 개의 독립적인 확률 변수의 합은 정규 분포를 따름.

정규 분포가 적용되는 예시
- 사람들의 키, 몸무게, 시험 점수
- 제조된 제품의 크기 변화 (품질 관리)
- 주식 시장의 가격 변동
- 기온 변화, 혈압, 심박수 등 생체 데이터
정규 분포의 확률 밀도 함수 (PDF)

여기서:
- μ = 평균 (Mean, 정규 분포의 중심)
- σ2 = 분산 (Variance, 데이터의 퍼짐 정도)
- σ = 표준편차 (Standard Deviation)
- e = 자연상수 (≈ 2.718)
정규 분포의 그래프는 평균을 중심으로 대칭적이고, 종 모양을 가진다.
표준 정규 분포 (Standard Normal Distribution)
- 정규 분포 중에서 평균이 0, 표준편차가 1인 경우를 표준 정규 분포(N(0, 1))라고 한다,
- 표준 정규 분포를 사용하면 모든 정규 분포를 동일한 기준에서 비교가 가능하다.
Z-점수 변환 (Z-score Transformation)
모든 정규 분포는 다음 변환을 통해 표준 정규 분포로 변환할 수 있다:
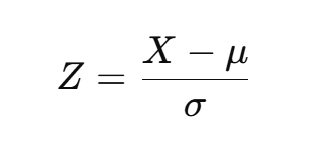
Z-값을 이용하면 정규 분포의 확률을 표준 정규 분포표(Z-Table)에서 쉽게 찾을 수 있다.
정규 분포의 누적 분포 함수 (CDF)
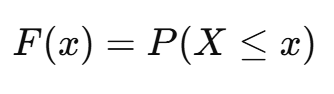
CDF는 적분을 이용해 구하지만, 보통 표준 정규 분포표(Z-Table)를 사용해서 값을 찾는다.
정규 분포의 68-95-99.7 법칙
정규 분포에서는 다음과 같은 법칙이 성립한다:
68-95-99.7 규칙 (Empirical Rule)
- 평균 ± 1σ → 전체 데이터의 68% 포함
- 평균 ± 2σ → 전체 데이터의 95% 포함
- 평균 ± 3σ → 전체 데이터의 99.7% 포함
즉, 대부분의 데이터는 평균 근처에 분포하고 있다. 이 법칙을 이용하면 데이터가 이상값(Outlier)인지 쉽게 판단이 가능하다.
정규 분포의 기댓값과 분산
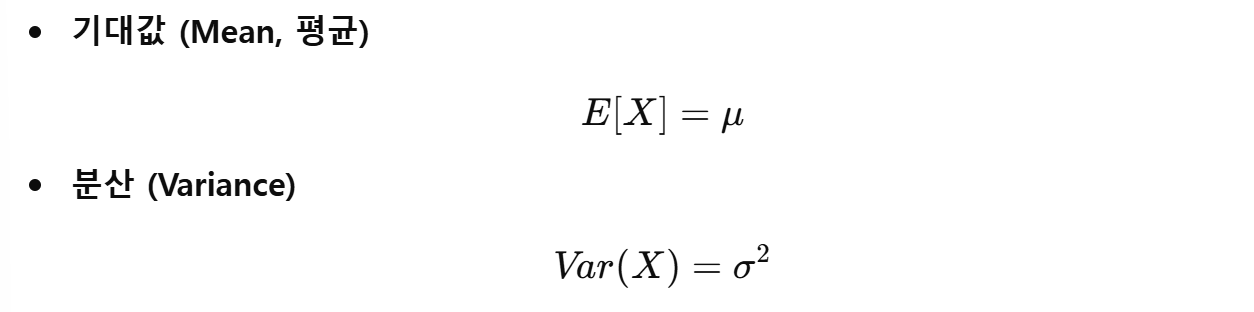
정규 분포의 활용
- 데이터 분석 & 통계 모델링
- 오차 분석 (Error Analysis)
- 머신러닝 & 인공지능 (Gaussian Naive Bayes, PCA 등)
- 자연 현상 분석 (온도, 시험 점수, 경제 데이터 등)
정규 분포는 현실 세계에서 가장 많이 등장하는 분포이다. 통계적 가설 검정 & 머신러닝에서 필수적으로 사용된다.
예제: 정규 분포(Normal Distribution)의 CDF
확률 변수 X∼N(μ, σ2) (평균 μ, 분산 σ2)를 따를 때, CDF를 구하자.
확률 밀도 함수(PDF):
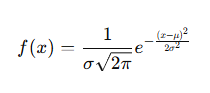
CDF 계산:
정규 분포의 CDF는 닫힌 형태(Closed-form solution)로 적분할 수 없다. 따라서, 표준 정규 분포표(Z-Table) 또는 누적 분포 함수 근사식을 이용해서 계산해야 한다.
즉, 특정 값 x의 누적 확률을 직접 적분하는 것이 아니라 표를 참고해서 빠르게 계산한다.
'데이터 사이언스 > 수리 통계학' 카테고리의 다른 글
| Change of Variables (확률 변수 변환) (0) | 2025.03.27 |
|---|---|
| The Laplace Distribution (라플라스 분포, 이중 지수 분포) (0) | 2025.03.26 |
| The Exponential Distribution (지수 분포) (0) | 2025.03.24 |
| The Uniform Distribution (균등 분포) (0) | 2025.03.23 |
| Probability Density Function and Cumulative Distribution Function (확률 밀도 함수와 누적 분포 함수) (0) | 2025.03.22 |




