- 큐
- 스택
- Article & User
- Tree
- Django
- 완전검색
- ORM
- regexp
- 쟝고
- SQL
- create
- distinct
- drf
- DB
- Queue
- Vue
- update
- migrations
- 통계학
- N:1
- 백트래킹
- 트리
- M:N
- count
- 뷰
- 이진트리
- outer join
- delete
- 그리디
- stack
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
데이터 분석 기술 블로그
Change of Variables (확률 변수 변환) 본문
확률 변수 변환(Change of Variables)은 주어진 확률 변수 X를 새로운 확률 변수 Y로 변환할 때의 확률 분포를 찾는 과정이다.
확률 변수 변환이 중요한 이유는:
- 새로운 변수를 정의해서 확률 분포를 바꿔야 하는 경우가 많음.
- 예를 들어, 데이터 변환(로그 변환, 제곱근 변환 등)을 할 때 사용됨.
- 머신러닝, 신호 처리, 경제 모델링 등 다양한 분야에서 활용됨.

확률 밀도 함수(PDF) 변환
만약 확률 변수 X가 주어졌을 때, 새로운 확률 변수 Y를 다음과 같이 변환한다고 하자:
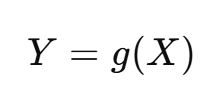
이때, Y의 확률 밀도 함수(PDF) fY(y)를 구하려면 다음 공식을 사용해야 한다.
- 단조 증가함수(Monotonic Increasing Function) 일 경우
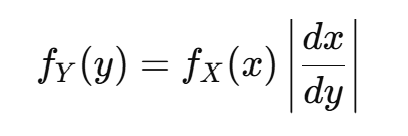
- 단조 감소 함수(Monotonic Decreasing Function)일 경우
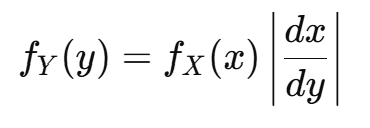
(변환이 단조 감소하는 경우도 절댓값을 취하면 된다.)
즉, 새로운 변수의 확률 밀도를 구하려면 원래 변수의 밀도에 변환 함수의 미분을 곱해줘야 한다.
다변수 확률 변수 변환 (Multivariable Change of Variables)
여러 개의 확률 변수가 있을 때, 이를 새로운 변수로 변환하는 과정에서 야코비 행렬(Jacobian Matrix)을 사용해야 한다.
두 개의 확률 변수 (X, Y)를 새로운 변수 (U, V)로 변환하는 경우
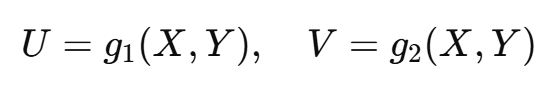
이때, 새로운 확률 밀도 함수 fU,V(u,v)f_{U,V}(u,v)는 다음과 같이 계산된다:
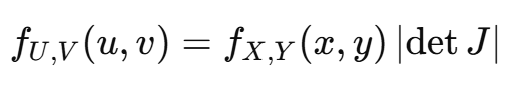
여기서 야코비 행렬(Jacobian Matrix)은 다음과 같다:

즉, 확률 밀도 함수 변환 시 야코비 행렬의 행렬식을 곱해줘야 한다.
예제 1: 정규 분포에서 제곱 변환
X ∼ N(0, 1) (표준 정규 분포)를 따르는 경우,
새로운 변수 Y = X2의 분포를 찾아보자.
PDF 정의
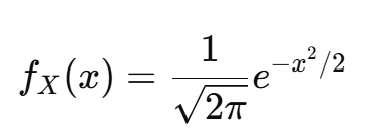
변환 함수 및 미분 계산
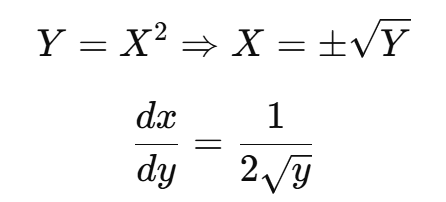
확률 밀도 함수 변환 적용

즉, Y = X2의 분포는 카이제곱 분포(Chi-Square Distribution)와 유사한 형태를 가진다.
예제 2: 균등 분포에서 로그 변환
X ∼ U(1, e) (균등 분포)일 때,
Y = lnX의 분포를 찾아보자.
PDF 정의
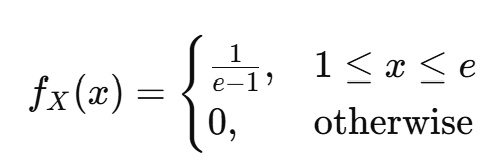
변환 함수 및 미분 계산
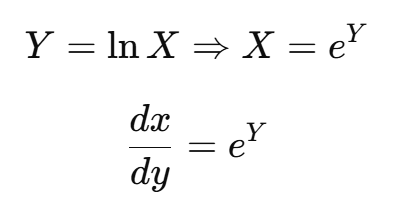
확률 밀도 함수 변환 적용
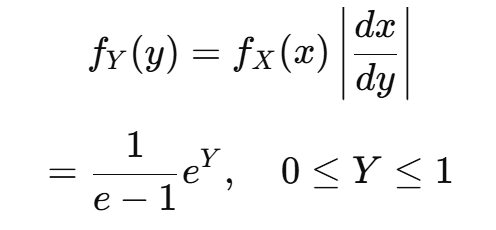
즉, 로그 변환된 데이터는 지수 분포와 유사한 형태를 가진다.
예제 3: 원 좌표계 변환 (Polar Coordinates)
확률 변수 (X, Y)가 정규 분포 N(0, 1)를 따를 때, 이를 극좌표계(Polar Coordinates)로 변환해보자.
변환식
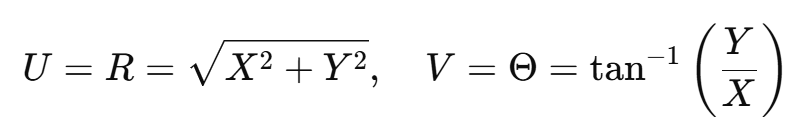
야코비 행렬 계산

변환 후 확률 밀도 함수
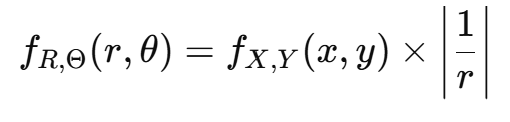
즉, 원형 좌표계로 변환할 때 밀도 함수가 반지름에 따라 조정된다.
예제 4: 선형 변환 (Linear Transformations)
다변수 정규 분포를 따르는 확률 변수 벡터 X에 선형 변환을 적용할 때의 확률 밀도를 찾아보자.
변환식
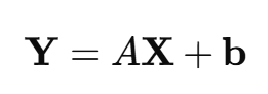
확률 밀도 함수 변환
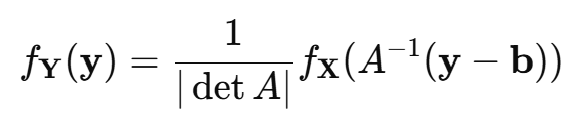
즉, 선형 변환을 적용하면 확률 밀도가 변하지만, 야코비 행렬식의 역수를 곱해줘야 한다.
'데이터 사이언스 > 수리 통계학' 카테고리의 다른 글
| Marginal of Bivariate Normal (이변량 정규분포의 주변 분포) (0) | 2025.03.29 |
|---|---|
| Joint and Marginal Distributions (결합 및 주변 분포) (0) | 2025.03.28 |
| The Laplace Distribution (라플라스 분포, 이중 지수 분포) (0) | 2025.03.26 |
| The Normal Distribution (정규 분포, Gaussian Distribution) (2) | 2025.03.25 |
| The Exponential Distribution (지수 분포) (0) | 2025.03.24 |




