Tags
- drf
- 뷰
- 통계학
- 큐
- count
- delete
- 스택
- outer join
- update
- Django
- create
- stack
- Article & User
- N:1
- ORM
- regexp
- 완전검색
- 트리
- M:N
- DB
- SQL
- 그리디
- Queue
- 이진트리
- 백트래킹
- migrations
- distinct
- Vue
- 쟝고
- Tree
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
Infinitely Many Solutions (무수히 많은 해) 본문
연립 선형 방정식이 무수히 많은 해를 가지는 경우는, 모든 방정식을 만족시키는 해가 하나가 아니라 무한히 존재할 때입니다.
이는 식들 간에 의존성(종속성)이 있어서 실제로는 독립적인 정보가 부족할 때 발생합니다.
예시

두 번째 식은 첫 번째 식을 2배 한 것입니다. 즉, 두 식은 같은 직선을 나타냅니다.
따라서 x + y = 2를 만족하는 모든 점이 해가 되며, 무한히 많은 해를 갖습니다.
행렬 표현
위 식을 행렬로 나타내면:

가우스 소거법 적용:
R2 = R2 - 2 × R1
→ [2, 2, 4] − 2 × [1, 1, 2] = [0, 0, 0]
결과:

즉, 독립적인 식은 1개뿐이고, 나머지는 중복 정보입니다. 해가 하나로 결정되지 않기 때문에, 자유 변수(free variable)를 두고 표현해야 합니다.
해를 일반화해서 표현

따라서 해는 다음과 같이 표현됩니다:
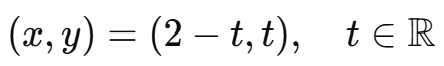
→ 변수 에 어떤 값을 넣든 항상 방정식을 만족하므로, 해는 무한히 많습니다.
기하학적 해석
- 2개의 방정식 → 같은 직선
- 3개의 방정식 → 같은 평면이거나, 평면들이 한 선을 공유
→ 모든 해는 공통된 선 또는 평면 위에 존재하게 됩니다.
요약

'데이터 사이언스 > 선형대수학' 카테고리의 다른 글
| Adding and Subtracting Vectors (벡터의 덧셈과 뺄셈) (0) | 2025.05.09 |
|---|---|
| What is a Vector? (벡터란 무엇인가?) (0) | 2025.05.08 |
| No Solutions (해가 없는 경우) (0) | 2025.05.06 |
| Gaussian Elimination (가우스 소거법) (0) | 2025.05.05 |
| Equations and 3 Unknowns (3개의 방정식과 3개의 미지수) (0) | 2025.05.04 |




