Multidimensional Change of Variables - Discrete (다변량 변수 변환 – 이산형)

이산형 확률 변수들이 여러 개일 때, 그들을 변환했을 경우 확률이 어떻게 바뀌는지 알아보자.

---

기본 개념

여러 개의 이산 확률 변수 X₁, X₂, …, X_n가 있을 때,
이들을 어떤 함수로 변환하여 새로운 확률 변수 Y₁, Y₂, …를 정의할 수 있어.

---

확률 계산 방식

변환된 변수 Y의 확률을 구하려면,
원래 변수 공간에서 Y = y를 만족하는 모든 (x1, x2, … ) 조합의 확률을 더해서 구해야 해 한다.

즉, 다대일 함수일 경우, 하나의 y에 해당하는 여러 x 값을 모두 더한다.

---

예제 1: 두 이진 변수의 합

 

 

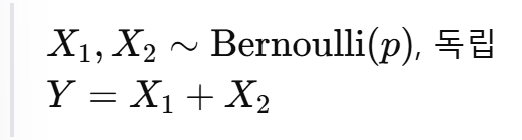
Y ∼ Binomial(2, p)
→ 이항 분포로의 변환

---

예제 2: 다항 분포 → 범주 합치기

 

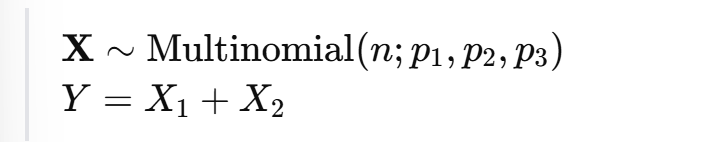
→ Y는 X₁, X₂​ 범주의 총합 (ex: "찬성 + 보통")

Y ∼ Binomial(n, p₁ + p₂)