데이터 분석 기술 블로그

Convolution From Adding Random Variables (확률 변수의 합과 컨볼루션) 본문

데이터 사이언스/수리 통계학

Convolution From Adding Random Variables (확률 변수의 합과 컨볼루션)

데이터분석가 이채은 2025. 4. 6. 02:01

문제 정의

두 연속 확률 변수 X, 의 합:

 

이때 Z의 확률 밀도 함수 fZ(z)는 다음과 같이 계산된다:

 

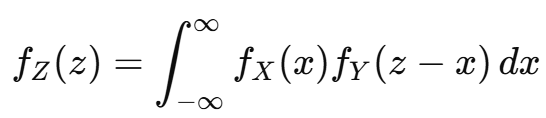
이게 바로 연속 확률 변수의 컨볼루션(convolution) 공식이다.

이산 확률 변수의 컨볼루션

이산형에서는 합 대신 합성곱(SUM of PMFs)을 사용한다:

 

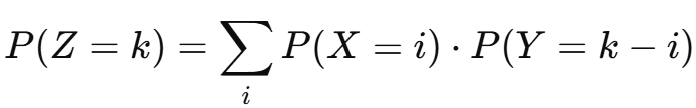
→ 실제로는 두 PMF를 디스크리트 컨볼루션(discrete convolution)하는 것과 동일

예제 1: 균등 분포 U(0, 1) + U(0, 1)

예제 2: 정규분포의 합

 

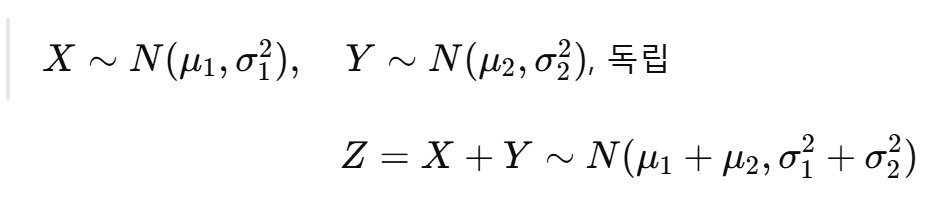
정규분포는 합을 취해도 정규분포 형태 유지
→ 굳이 적분할 필요 없이 공식으로 해결 가능

'데이터 사이언스 > 수리 통계학' 카테고리의 다른 글

Expected Value and Mean (기댓값과 평균)  (0) 2025.04.07
Multidimensional Change of Variables - Continuous (다변량 변수 변환 – 연속형)  (0) 2025.04.05
Multidimensional Change of Variables - Discrete (다변량 변수 변환 – 이산형)  (0) 2025.04.04
Multinomial Distribution (다항 분포)  (0) 2025.04.03
Multivariate Normal Distribution / Vector Gaussian (다변량 정규분포)  (0) 2025.04.02
'데이터 사이언스/수리 통계학' Related Articles more