Tags
- delete
- outer join
- create
- Article & User
- 통계학
- 백트래킹
- Django
- N:1
- DB
- stack
- distinct
- 이진트리
- migrations
- Vue
- update
- 스택
- drf
- Queue
- SQL
- M:N
- Tree
- 완전검색
- 큐
- 뷰
- 쟝고
- 그리디
- ORM
- regexp
- 트리
- count
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
The Vector Normal to a Plane (평면의 법선 벡터) 본문
평면의 법선 벡터(normal vector)는 그 평면에 수직인 방향을 가지는 벡터입니다.
즉, 평면을 뚫고 나오는 방향을 가진 벡터라고 생각하시면 됩니다.
법선 벡터는 평면을 나타내는 방정식과 밀접한 관계가 있습니다.
응용 예
- 평면과 점 사이의 거리 계산
- 평면 위의 벡터 투영
- 교차 여부 판단 (벡터와 평면의 수직 조건 등)
- 컴퓨터 그래픽스에서 표면 방향 계산
- 머신러닝에서 decision boundary의 방향성 이해
3차원에서 일반적인 평면 방정식은 다음과 같습니다:
여기서 a, b, c는 각각 x, y, z에 대한 계수이며,
이 세 수를 이용해 다음과 같이 법선 벡터를 만들 수 있습니다:
즉, 평면의 방정식에서 변수 앞의 계수들이 바로 법선 벡터를 이룹니다.
예제
다음 평면을 보겠습니다:

이때 법선 벡터는:
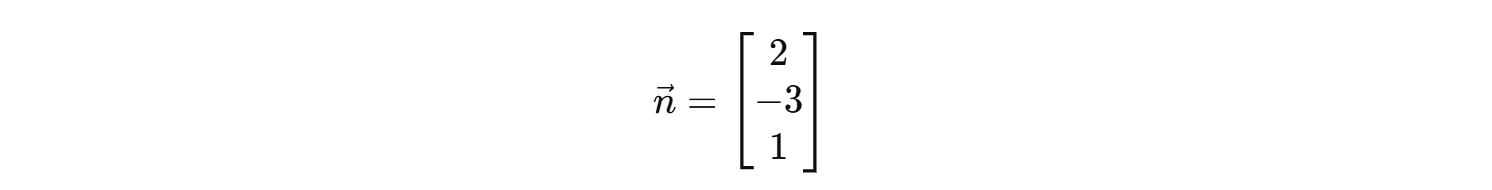
이 벡터는 해당 평면에 수직이며, 기하학적으로는 해당 평면과 직각을 이루는 방향을 나타냅니다.
두 벡터의 외적을 통한 법선 벡터
벡터 두 개가 평면 위에 있다고 할 때, 그 두 벡터의 외적(cross product)을 계산하면 그 결과가 해당 평면의 법선 벡터가 됩니다.
예:

→ x축과 y축을 이루는 평면의 법선은 z 축 방향.
'데이터 사이언스 > 선형대수학' 카테고리의 다른 글
| Matrix Addition and Scalar Multiplication (행렬의 덧셈과 스칼라 곱) (0) | 2025.05.15 |
|---|---|
| What is a Matrix? (행렬이란 무엇인가?) (0) | 2025.05.14 |
| Normalizing a Vector (벡터 정규화) (0) | 2025.05.12 |
| Properties of Dot Product (내적의 성질) (0) | 2025.05.11 |
| Dot Product (내적, 또는 스칼라 곱) (0) | 2025.05.10 |




